Het Toepassen van Reinforcement Learning op Order-Pick Routing in Magazijnen

Introductie tot Reinforcement Learning  

Reinforcement Learning is een hot topic op het gebied van machine learning. Denk aan zelfrijdende auto’s of bots die complexe spellen spelen. Echter, de toepassing van deze techniek op operationele problemen is schaars. In deze blogpost leiden we je door de basisconcepten van Reinforcement Learning en hoe het kan worden gebruikt om een eenvoudig order-pick routing probleem in een magazijn op te lossen met behulp van Python.

Reinforcement Learning is een hot topic op het gebied van machine learning en kan worden toegepast op een breed scala aan problemen. Zoals geformuleerd door Bhatt: “Reinforcement Learning (RL) is een type machine learning techniek die een agent in staat stelt te leren in een interactieve omgeving door middel van trial-and-error, gebruikmakend van feedback van zijn eigen acties en ervaringen.” RL is een vorm van unsupervised learning, wat betekent dat het geen gelabelde input- en outputdata nodig heeft.

Een typisch RL-probleem wordt gemodelleerd als een MDP en bestaat uit:

• Omgeving: De wereld waarin de agent opereert.
• Staat: Huidige situatie van de omgeving, de verzameling van staten wordt aangeduid met S.
• Actie: Een beslissing die de agent neemt en die de omgeving beïnvloedt en de huidige staat verandert, de verzameling van acties wordt aangeduid met A. De verzameling van acties kan ook uniek worden gedefinieerd voor elke staat s ∈ S en wordt aangeduid als A(s).
• Beloning: Feedback van de omgeving, de beloning na de overgang van staat s naar staat s′ met actie a wordt aangeduid met ra(s, s′).
• Staat-actie-overgangswaarschijnlijkheid: Waarschijnlijkheid van de overgang van staat s naar staat s′ onder actie a aangeduid met p(s′|s, a). De verzameling van waarschijnlijkheden wordt aangeduid met P.

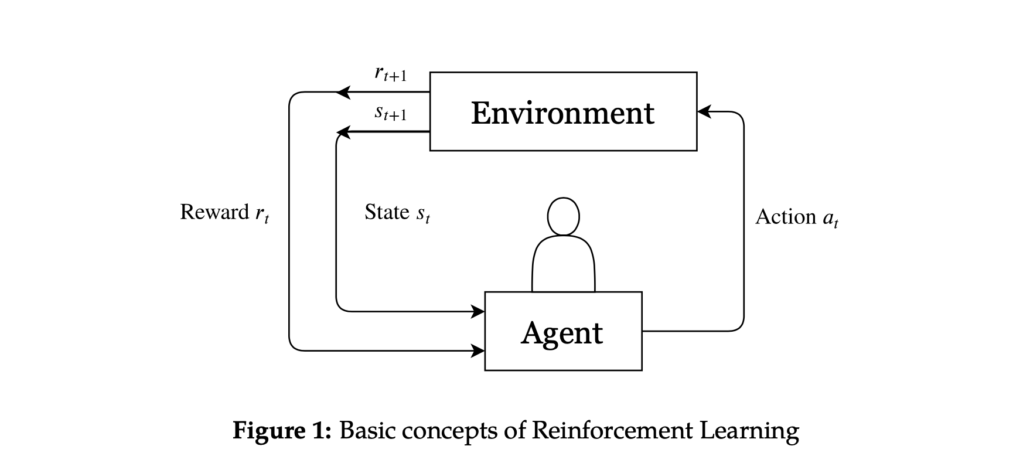
Deze concepten worden geïllustreerd in figuur 1. Op elk discrete tijdstip t, interacteert de agent met de omgeving door de huidige staat st te observeren en een actie at te ondernemen uit de verzameling beschikbare acties. Na het uitvoeren van een actie gaat de omgeving over naar een nieuwe staat st+1 en observeert de agent een beloning rt+1 geassocieerd met de overgang (st, at, st+1). Het uiteindelijke doel van de agent is om de toekomstige beloning te maximaliseren door te leren van de impact van zijn acties op de omgeving. Op elk tijdstip moet de agent een afweging maken tussen de lange termijn beloning en de korte termijn beloning.

Vanwege zijn generaliteit kan Reinforcement Learning worden toegepast op een breed scala aan problemen. Bijvoorbeeld, RL wordt vaak gebruikt bij het bouwen van AI voor het spelen van computerspellen zoals Pacman, Backgammon en AlphaGo, maar ook voor het ontwerpen van software voor zelfrijdende auto’s.

Order-Pick Routing Geformuleerd als een RL-Probleem  

Nu we de kernconcepten van een RL-probleem kennen, willen we weten hoe we ons order-pick routing probleem naar deze kernconcepten kunnen vertalen.

Order-picking in een magazijn kan worden gezien als een speciale vorm van het klassieke Traveling Salesman Problem (TSP) dat vraagt: “Gegeven een lijst van steden en de afstanden tussen elk paar steden, wat is de kortst mogelijke route die elke stad bezoekt en terugkeert naar de beginstad?”. Vertaald naar order-pick routing, wordt deze vraag met andere terminologie: “Gegeven een lijst van picklocaties en de afstanden tussen elk paar picklocaties, wat is de kortst mogelijke route die elke picklocatie bezoekt en terugkeert naar het I/O-punt?”. Het TSP is een veel bestudeerd probleem in het veld van combinatorische optimalisatie en veel heuristieken zijn ontwikkeld om het TSP op te lossen. Hier proberen we het magazijn order-pick routing te formuleren als een MDP:

Een werknemer met een karretje (agent) reist door het magazijn (omgeving) om een set van pick-nodes te bezoeken. De agent beslist op elk tijdstip t welke node als volgende wordt bezocht, waarbij de geselecteerde node van ongebruikt naar gebruikt verandert (staat). De agent probeert de beste volgorde van de nodes te leren, zodanig dat de negatieve totale afstand (beloning) wordt gemaximaliseerd. De kernconcepten van deze MDP zijn als volgt:

• Staat: Een representatie van de magazijnomgeving met de huidige node en een set van ongebruikte nodes. st bevat de huidige node en een lijst van nodes die nog bezocht moeten worden.
• Actie: Een eindige set van acties A van het selecteren van de volgende node die bezocht moet worden. A zou de set van alle nodes kunnen zijn en hetzelfde voor elke staat s of afhankelijk zijn van s waarbij de set van mogelijke acties in de loop van de tijd afneemt. In het laatste geval, wanneer alle nodes bezocht zijn op tijdstip t, is de enige mogelijke actie at om terug te keren naar het I/O-punt.
• Beloning: Feedback van de omgeving, de beloning na de overgang van staat s naar staat s′ met actie a is altijd de negatieve afstand tussen nodes s en s′ behalve voor de terminale staat. Bij de terminale staat ontvangt de agent een extra grote beloning voor het voltooien van zijn route.
• Staat-actie-overgangswaarschijnlijkheid: Waarschijnlijkheid van overgang van staat s naar staat s′ onder actie a aangeduid met p(s′|s, a). Voor elke actie weten we wat de volgende staat zal zijn, dus p(s′|s, a) = 1 voor een vooraf bekende staat s′ en 0 voor alle andere staten.

Nu zullen we deze concepten illustreren met een klein voorbeeld van een magazijn dat we modelleren in Python.

Klein Voorbeeld Gemodelleerd in Python  

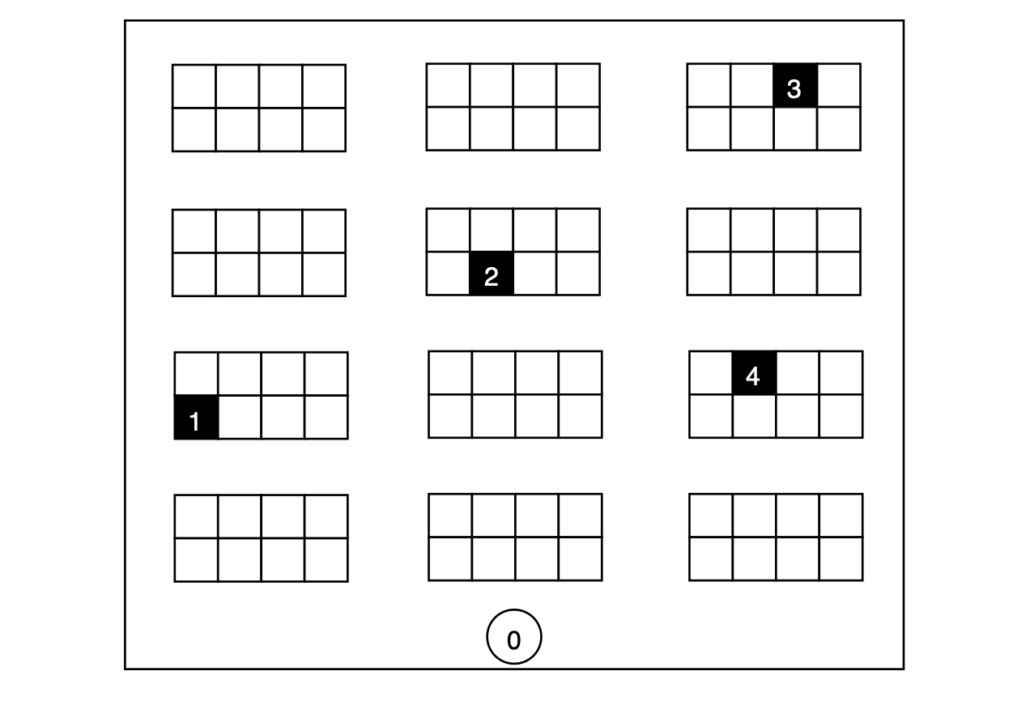
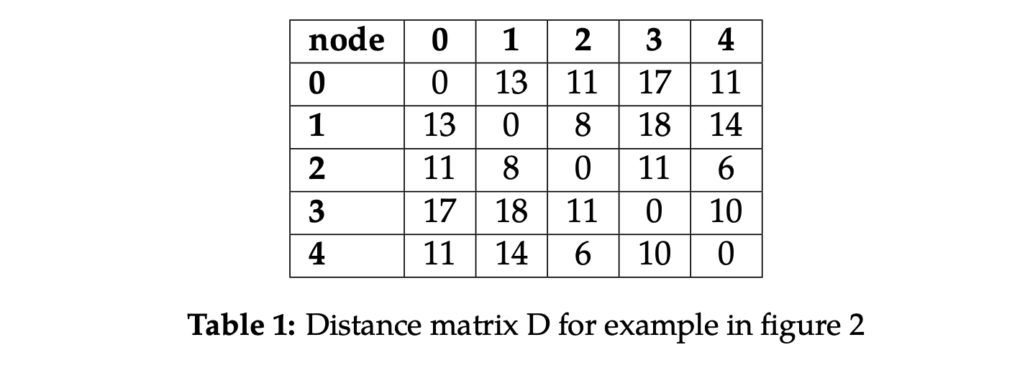
Stel dat we een magazijn hebben met een lay-out zoals in figuur 2. Nu krijgt de agent een order en moet hij in totaal vier producten op verschillende locaties ophalen. We nummeren de picklocaties van 1 tot 4 en geven de startlocatie aan als locatie 0. Door de structuur van het magazijn kunnen we de kortste paden tussen alle punten berekenen en deze opslaan in de afstandsmatrix D van formaat 5 bij 5 (zie tabel 1).

Begeleiding  

Het concrete doel van de agent is om alle picklocaties te bezoeken en terug te keren naar de startlocatie op de kortst mogelijke manier. Voor dit specifieke voorbeeld is het gemakkelijk om de optimale volgorde van nodes te berekenen door simpelweg alle mogelijkheden door te nemen, 4! = 24 in totaal. Aangezien we de optimale route kennen, kunnen we eenvoudig controleren of onze agent in staat is om de optimale route te leren. Voor dit specifieke voorbeeld is de set van acties hetzelfde voor elke staat s ∈ S, dus A(s) = A voor alle s ∈ S en wordt gedefinieerd door:

$$A = \set{0,1,2,3,4}$$

Merk op dat dit betekent dat een agent kan besluiten om naar een pick-node te gaan die al bezocht is. Een staat wordt gedefinieerd door een tuple s = (is, Vs) bestaande uit de huidige locatie is en een set locaties Vs die nog bezocht moeten worden. Bijvoorbeeld, de staat s = (2, {1, 3}) betekent dat de agent zich op pick-locatie 2 bevindt en nog de pick-locaties 1 en 3 moet bezoeken. Formeel definiëren we de set van staten door:

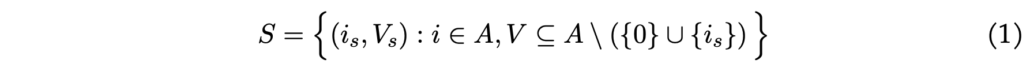
Merk op dat men handmatig kan verifiëren dat het totale aantal staten in dit voorbeeld gelijk is aan 48. In het algemeen, als we de set van staten op deze manier definiëren, is het aantal staten gelijk aan:

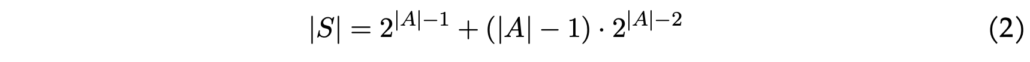
In vergelijking (2), als de agent zich op locatie 0 bevindt, zijn er 2∣A∣−12∣A∣−1 mogelijke lijsten van locaties die nog bezocht moeten worden. Voor de andere (∣A∣−1)(∣A∣−1) locaties zijn er 2∣A∣−22∣A∣−2 mogelijke lijsten van locaties die nog bezocht moeten worden. Voor elke gegeven toestand weten we voor elke actie wat de volgende toestand zal zijn. Bijvoorbeeld, als de agent zich in de toestand (0, {1, 2, 3, 4}) bevindt en besluit naar picklocatie 3 te gaan, is de volgende toestand (3, {1, 2, 4}). Formeel definiëren we de toestand-actie-transitie waarschijnlijkheid als:

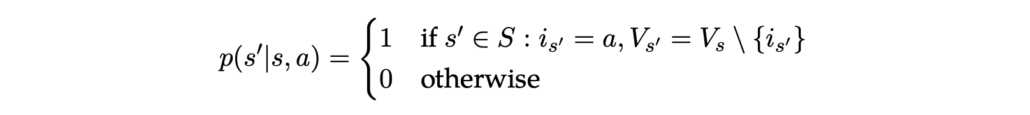
Nu rest alleen nog het definiëren van de beloningsfunctie. We geven de agent een negatieve beloning als hij van locatie xxnaar locatie yy gaat, gelijk aan min de afstand tussen xx en yy: −D(x,y)−D(x,y). Als hij terugkeert naar het startpunt nadat hij alle steden heeft bezocht, d.w.z. als hij de terminale toestand bereikt, ontvangt hij een grote beloning van 100 (of een ander relatief groot getal in vergelijking met de afstanden). Formeel wordt de beloning gegeven door:

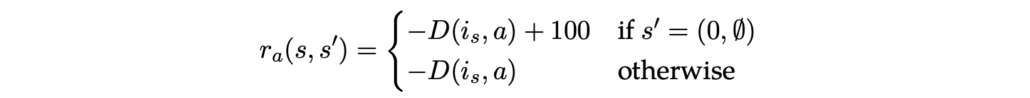
Python Code  

import itertools
import pandas as pd
from tabulate import tabulate
import random
from sklearn.metrics import euclidean_distances

# Initialize toy data
# 1 start point (0), 4 pick locations (1,2,3,4)

D = np.array([[0,13,11,17,11], [13,0,8,18,14], [11,8,0,11,6], [17,18,11,0,10], [11,14,6,10,0]])
# locations = [(5,0), (2,5), (4,5), (6,5), (8,5)]
# D = euclidean_distances(locations)*100
np.fill_diagonal(D, 999)

# Generate set of actions and set of pick-nodes
Actions = set(range(n))
Nodes = Actions.copy()
Nodes.remove(0)

# Generate all possible states
states = []
for j in range(n):
  if j > 0:
    subset = Nodes.copy()
  if j == 0:
    subset = Actions.copy()
  subset.remove(j)
  for i in range(len(subset)+1) :
    a = list(itertools.combinations(subset, i))
    for k in range(len(a)):
      states.append((j, a[k]))

# Define the state space transition matrix
Transition = np.zeros([len(states), n])
Transition = Transition.astype(int)

for i in range(len(states)):
  for j in range(n):
    new_set = set(states[i][1])
    new_set.discard(j)
    new_set = tuple(new_set)
    state = (j, new_set)
    Transition[i, j] = states.index(state)

# Now we want to define the reward matrix with negative distance
Reward = np.zeros([len(states), n])

for i in range(len(states)):
  for j in range(n):
    bonus = (i>0)*(len(state[i][1]) == 0 and j == 0)
    Reward[i, j] = -D[states[i][0], j] + bonus*100

Oplossen met Q-learning  

Er zijn verschillende reinforcement learning-algoritmen ontwikkeld om de agent te trainen. Het meest gebruikte algoritme heet Q-learning, geïntroduceerd door Chris Watkins in 1989. Het algoritme heeft een functie die een kwaliteitsmaatstaf berekent voor elke mogelijke staat-actie combinatie:

$$Q:S×A→R$$

De waarde Q(st, at) geeft, simpel gezegd, aan hoe goed het is om actie at te nemen terwijl je in staat st bent. Q-learning werkt iteratief de Q-waarden bij om de uiteindelijke Q-tabel met Q-waarden te verkrijgen. Uit deze Q-tabel kan men het beleid van de agent aflezen door in elke staat st de actie at te nemen die de hoogste waarden oplevert. Bijwerken gebeurt volgens de volgende regel:

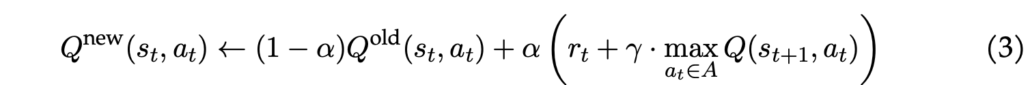
Het algoritme maakt gebruik van de volgende parameters/variabelen:

• Initiële waarden (Q0): Meestal worden de initiële Q-waarden op 0 gezet. Echter, als we exploratie willen stimuleren (een concept dat later in deze sectie wordt uitgelegd), moeten we relatief hoge initiële Q-waarden kiezen. Deze worden optimistische initiële waarden genoemd.
• Leerfactor (α): De leerfactor bepaalt hoeveel de agent leert. Een leerfactor van 0 betekent dat de agent niets leert en Q-waarden helemaal niet worden bijgewerkt. Een waarde van 1 betekent dat de agent alleen naar de meest recente informatie kijkt en de oude informatie vergeet.
• Kortingsfactor (γ): De kortingsfactor geeft aan hoeveel de agent naar toekomstige beloningen kijkt. Als γ = 0, kijkt de agent alleen naar de huidige beloning.

Als er een terminale staat is, stopt een episode van het algoritme als deze terminale staat is bereikt.

Het altijd nemen van de actie die de hoogste Q-waarde geeft in een bepaalde staat wordt een greedy policy genoemd. Echter, voor veel problemen kan het altijd selecteren van de greedy actie ervoor zorgen dat de agent vast komt te zitten in een lokaal optimum. Daarom maken we een onderscheid tussen exploitatie en exploratie:

• Exploitatie: In elke iteratie de actie selecteren die resulteert in de beste bekende beloning volgens een vooraf gedefinieerde functie.
• Exploratie: Een zet selecteren die niet noodzakelijkerwijs leidt tot de beste bekende beloning, wat meer informatie over de omgeving geeft. Dit kan een willekeurige actie zijn of een actie volgens een bepaalde waarschijnlijkheidsfunctie.

Een manier om de afweging tussen exploitatie en exploratie te implementeren, is door gebruik te maken van ε-greedy. Met waarschijnlijkheid 1 − ε kiest de agent de actie waarvan hij gelooft dat deze het beste langetermijneffect heeft (exploitatie) en met waarschijnlijkheid ε neemt hij een willekeurige actie (exploratie). Meestal is ε een constante parameter, maar deze kan in de loop van de tijd worden aangepast als men in de vroege stadia van training meer exploratie verkiest.

# *** Q - Learning ***
Q_table = np.ones([len(states), n])*1000

# Hyperparameters
alpha = 0.2
gamma = 0.9
epsilon = 0.3

# The algorithm
for i in range (400000):
  begin_state = (0, tuple(Nodes))
  state = states.index(begin_state)
  done = False

  while not done:
    if random.uniform(0, 1) < epsilon:
      action = random.randrange(n) # Explore action space
    else:
      action = np.argmax(Q_table[state]) # Exploit learned values

    next_state = Transition[state, action]
    reward = Reward[state, action]

    if state == states.index((0, ())):
      done = True

    old_value = Q_table[state, action]

    next_max = пр.max(Q_table[next_state])

    new_value = (1 - alpha) * old_value + alpha * (reward + gamma * next_max)
    Q_table[state, action] = new_value

    state = next_state

q_df = pd.DataFrame(Q_table)
q_df.index = states

Nu zullen we dit algoritme in Python implementeren om ons kleine order-pick routing voorbeeld op te lossen. Omdat we te maken hebben met een episodische omgeving met een terminale parameter, stellen we onze kortingsfactor γ = 0.9. We nemen de leerparameter α = 0.2 en de exploratieparameter ε = 0.3.

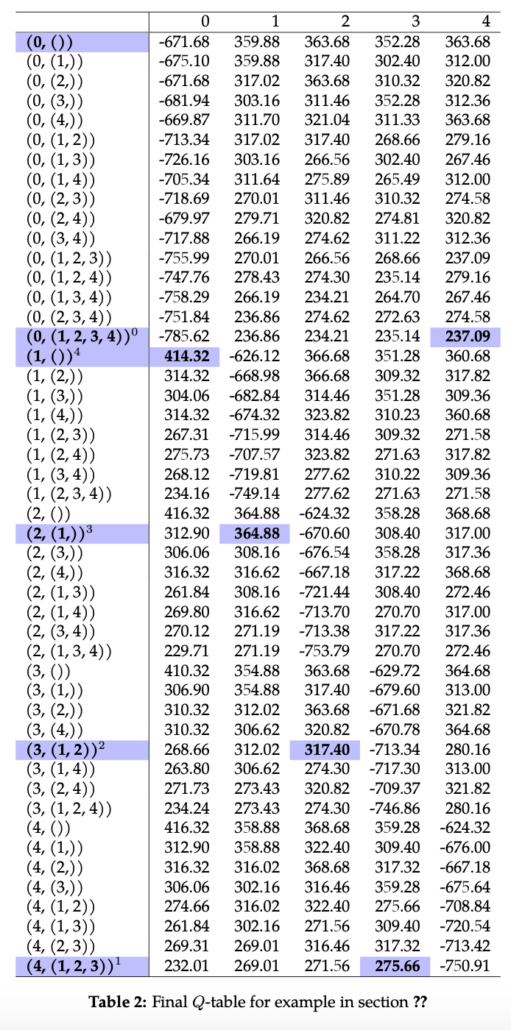
We draaien het algoritme totdat de Q-waarden convergeren en de uiteindelijke Q-tabel kan worden gevonden in tabel 2. Uit de tabel kunnen we de oplossing aflezen die met Q-learning is gevonden door de actie te selecteren die de hoogste waarde oplevert en de toestand-actie-overgang te volgen zoals gedefinieerd met de waarschijnlijkheden: 0 → 4 → 3 → 2 → 1 → 0. We zien dat de agent elke pick-node één keer bezoekt en terugkeert naar het startpunt. Bovendien is hij erin geslaagd de optimale oplossing te vinden!

Conclusie  

In deze blogpost hebben we een introductie gegeven tot Reinforcement Learning en laten zien hoe Q-learning kan worden gebruikt om een klein order-pick routing voorbeeld in een magazijn op te lossen. Om grotere routing voorbeelden op te lossen, explodeert het aantal toestanden en wordt het werken met een Q-tabel computationeel onhaalbaar. Neurale netwerken zouden kunnen worden gebruikt om dit probleem te overkomen. In plaats van een Q-tabel voor elk toestand-actie paar te gebruiken, wordt een neuraal netwerk getraind om de Q-waarden te schatten.